|
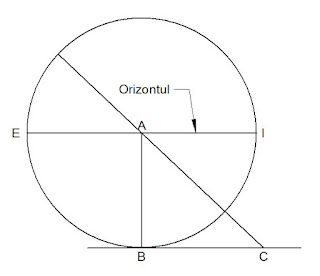
| Analema lui Vitruviu desenată pentru Cluj-Napoca |
Principala sursă de informație în ceea ce privește istoria și construcția cadranelor solare antice o constituie opera De architectura (Despre arhitectură) a lui Vitruviu (80/70 î.Hr-15 î.Hr.), mai exact cartea a IX-a, unde găsim o interesantă digresiune astronomică. Ne va interesa în mod special capitolul al VII-lea, intitulat "Despre traseul analemei". Ce este o analemă? Pe astronomii contemporani, fie ei amatori sau profesioniști, termenul îi duce cu gândul la diagrama în formă de 8 care le arată cât de mult se abate soarele adevărat de soarele mediu fictiv în decursul unui an. Fenomenul poate fi pus în evidență cu un aparat fotografic îndreptat spre sud cu care se expune câte un clișeu în fiecare zi, de exemplu la ora 12:00, observând schimbările zilnice de poziție ale astrului luminos. Un asemenea experiment fotografic interesant a fost realizat anii trecuți la Cluj-Napoca în premieră de către Pál Váradi Nagy. Sensul analemei lui Vitruviu se apropie însă mai mult de cel al unei leme matematice: un adevăr cunoscut ce reprezintă abia un pas intermediar în demonstrarea unui adevăr de mai largă circulație (teoremă) sau, în cazul nostru, o unealtă în vederea construirii cadranelor solare. Vom cita în continuare întreg capitolul relevant din traducerea românească a lui G.M. Cantacuzino, G. Ionescu și T. Costa, publicată în 1964, la care am adăugat propriile note explicative și grafice. Fragmentul începe la pag. 376 și continuă până la pag. 378.
Capitolul a VII-lea
Despre traseul analemei
"Lăsând deoparte considerațiile pe care le-am enunțat în capitolul precedent, să explicăm acum de ce se scurtează zilele după luni și modul cum le putem determina durata. În timpul echinocțiului, când Soarele se mișcă în Berbec și Cumpăna, dacă gnomonul e împărțit în nouă părți, sub înclinarea pe care o are cerul la Roma, sub efectul razelor soarelui el face o umbră egală cu 8 părți. În același timp, la Atena, umbra este mare cât trei din patru părți ale gnomonului; la Rodos, 5 din 7; la Tarent, 9 din 11; la Alexandria, 3 din 5. Și în toate celelalte locuri, umbrele echinoxiale ale gnomoanelor se află a fi lăsate de natură fiecare cu altă măsură."Vitruviu folosește raportul dintre lungimea umbrei și lungimea gnomonului (vergelei) la amiaza echinocțiilor pentru a ilustra diferența de latitudine între localități, cunoscut fiind faptul că un ceas solar fixează din punct de vedere constructiv unele elemente specifice latitudinii pentru care a fost conceput. Nouă însă ne e mai la îndemână să lucrăm cu grade latitudine și vom lua ca exemplu cazul municipiul Cluj-Napoca, situat la 46,77 grade nord față de ecuator. Cunoscând faptul că la echinocții soarele se află pe ecuatorul ceresc, iar acesta are la Cluj-Napoca înclinarea complementară de 90-46,77=43,23 grade față de orizontală, întrebarea este care raport dintre lungimea umbrei și lungimea gnomonului exprimă suficient de bine acest loc? După câteva încercări am găsit că raportul 17:16 se apropie destul bine de valoarea cotangentei lui 43,23, cu alte cuvinte pentru o vergea verticală de 16 cm înălțime lungimea umbrei la amiaza echinocțiilor va atinge 17 cm la Cluj-Napoca. În text Vitruviu operează cu valorile pentru Roma, dar noi vom folosi în continuare valorile pentru orașul nostru, adaptând instrucțiunile și construind astfel analema vitruviană pentru Cluj-Napoca.
"Așadar, în orice loc unde trebuie trasat un orologiu, trebuie luată acolo umbra echinoxială și, dacă sunt, ca la <Cluj-Napoca>, <șaisprezece> părți de gnomon și <șaptesprezece> de umbră, să se traseze o linie de pământ și, din mijlocul ei, să se ridice o vergea verticală, care e numită gnomon. Apoi, pornind de la linia de pământ, să se măsoare pe linia gnomonului, cu compasul <șaisprezece> părți și în locul în care se va găsi semnul părții a <șaisprezecea> să se stabilească un centru, acolo unde va fi litera A. Mai departe, deschizând compasul de la acest centru și până la linia pământului, unde va fi litera B, să se descrie o circumferință de cerc, care e numită meridiană."Cercul va reprezenta în desen secțiunea meridianului locului (direcția nord-sud) văzută din lateral.
"Apoi, din cele <șaisprezece> părți care sunt de la linia de pământ până la centrul gnomonului, să se ia <17>, însemnându-le pe linia de pământ unde va fi litera C. Aceasta va fi umbra echinoxială a gnomonului. De la acest semn și literă C, prin centru, unde e litera A, să se tragă o linie. Aceasta este raza echinoxială a Soarelui."Raza echinoxială (sau echinocțială) a soarelui o identificăm azi cu planul ecuatorului ceresc, adică prelungirea pe bolta cerească a planului ecuatorului terestru. Raza echinoxială o putem privi ca fenomen luminos și ca element geometric.
"Atunci, cu o deschidere de compas egală cu distanța de la centru până la linia pământului, să se determine o linie de echidistanță unde va fi litera E în partea stângă și I în partea dreaptă, pe linia circumferinței. Ea trebuie trasată prin centru, pentru ca circumferința să fie împărțită în două semicercuri egale. Linia aceasta e numită de matematicieni Orizont."Orizontul desenat pe hârtie este planul orizontului văzut din lateral.
"Apoi, din circumferința întreagă se ia a 15-a parte și așezând un vârf de compas pe linia de circumferință a locului în care raza echinoxială taie această linie, unde va fi litera F, să se facă semne în dreapta și în stânga, unde sunt literele G și H."A cincisprezecea parte de cerc (360/15=24) corespunde valorii rotunjite pentru înclinarea axei terestre sau oblicitatea eclipticii, adică unghiul dintre planul sistemului solar și planul ecuatorului terestru (valoarea mai apropiată pentru epoca noastră este 23,4 grade). Filmulețul de mai jos prezintă de la minutul 1:51 modul în care cercul se poate împărți în 15 părți egale folosind doar o riglă și un compas.
"Apoi, plecând din centrul A să se tragă prin aceste puncte două linii, prelungindu-le până la linia de pământ, unde vor fi literele R și T. Acestea vor fi razele soarelui: una de iarnă, cealaltă de vară. În fața lui E va fi litera I, unde circumferința e tăiată de linia care trece prin centrul liniei orizontului. Opuse literelor G și H vor fi K și L, iar opuse literelor C și F și A va fi litera N."
"Din G la L și din H la K să se traseze două transversale. Cea de deasupra se află în partea Verii, cea de dedesubt a Iernii. Aceste transversale trebuie să fie împărțite în două părți egale, unde vor fi literele O și M, Acolo se vor însemna centre. Și, trecând prin aceste semne și prin centrul A, să se ducă o linie până unde se va intersecta cu circumferința, unde se vor pune litere Q și P. Această linie va fi perpendiculară pe raza echinoxială și, după terminologia matematică, ea poartă numele de axa lumii."Axa lumii reprezintă axa terestră, în jurul căreia pare să se rotească întreaga sferă cerească, când, de fapt, cu toții știm că Pământul este cel care se rotește. Adevărul heliocentric interesează aici mai puțin deoarece urmărim în primul rând efectul perceput de observator.
"Din cele două centre O și M, cu o deschidere de compas întinsă până la extremitățile transversalelor LG și KH, să se descrie două semicercuri. Unul din ele va fi cel de vară, celălalt cel de iarnă."Rostul acestor două semicercuri este poate cel mai greu de înțeles din toată construcția geometrică, dar, dacă ne imaginăm desenul în 3D, cercul fiind bolta cerească văzută din lateral, cu sudul în stânga, nordul in dreapta și privrea dinspre est spre vest, atunci pe această sferă cele două semicercuri ridicate din planul hârtiei într-un plan perpendicular pe ea vor reprezenta jumătate de traseu solar (cealaltă jumătate aflându-se în planul îndepărtat), unul vara (superior) celălalt iarna (inferior). Traseul solar cuprinde o parte de zi în care astrul se ridică deasupra orizontului și o parte de noapte în care acesta este invizibil, coborând sub orizont. Se poate astfel observa ușor că vara soarele petrece mai mult timp deasupra orizontului EI și iarna mai puțin.
"În locurile unde liniile paralele (cele două transversale) taie linia numită Orizont, în partea dreaptă va fi litera S, în stânga V."În desen linia EI fiind de fapt planul orizontului, intersecțiile cu aceasta a diametrelor semi-arcurilor în S și V vor reprezenta punctele de răsărit/apus ale soarelui la solstițiul de vară, respectiv solstițiul de iarnă.
"Și de la litera G o linie paralelă cu axa se va duce până la extremitatea din dreapta a semicercului, unde va fi litera H. Această linie paralelă e numită locothomus. Apoi, cu piciorul compasului așezat în locul unde raza echinoxială taie această linie GH, unde va fi litera D, să se traseze - cu o rază egală cu distanța de la litera D, unde e centrul echinoxial, până unde raza de vară taie circumferința, unde e litera H - o circumferință care va fi cercul lunilor, numit Menaeus."Dacă cercul mai mic, botezat Menaeus (atenție, cu centrul în D și nu în F ca cercul ajutător desenat anterior), se împarte în 12, iar părțile obținute sunt marcate succesiv cu semnele zodiilor începând cu Racul în G sau Capricornul în H (direcția nu contează), se obține cercul zodiacal complet. La ce ajută acesta vom vedea într-un material viitor. Pe scurt, Menaeus-ul ne va permite stabilirea înălțimii soarelui și deci și a lungimii umbrelor la mijlocul oricărei zile alese din an, după poziționarea punctului pe cerc în cadrul intervalului zodiei.
"Astfel se face traseul analemei. Acestea fiind astfel trasate și explicate, cu ajutorul liniilor de vară sau de iarnă sau de echinox sau chiar de luni, după ipoteze, se va determina raportul orelor, prin traseuri după analemă. Se introduc aci ca ipoteze și multele varietăți și feluri de orologii și pentru toate cadranele se trasează după aceste procedee ingenioase. Într-adevăr, scopul tuturor figurilor și traseelor este același, ca ziua echinoxială sau cea mai scurtă sau cea a solstițiului să fie împărțită deopotrivă în douăsprezece părți egale. Peste aceste lucruri însă am trecut, dar nu împiedicat de lene, ci ca să nu plictisesc, scriind prea multe."Vedem așadar că tratamentul lui Vitruviu este incomplet, el nu duce "demonstrația" până la capăt, nu prezintă concret modul de lucru prin care analema era folosită în construcția cadranelor solare, de frică să nu plictisească. Putem astfel intui că respectivele informații erau deja arhi-cunoscute cititorilor săi. În decursul timpului au existat mai multe propuneri de a completa informațiile lipsă ale lui Vitruviu în scopul realizării unui cadran solar, iar într-un articol viitor ne propunem să ilustrăm una dintre aceste metode.